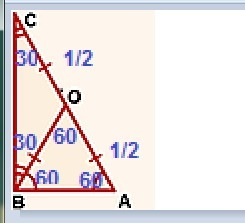
1. Медиана делит прямой угол в отношении 1:2: 1х+2х=90°
3х=90°
х=30°; 2х=60°
2. Медиана, опущенная из прямого угла к гипотенузе, делит гипотенузу пополам.
2. Если длина медианы равна длине одного из катетов, то получает равнобедренный треугольник, углы в основании которого равны:
если ∠ОВА=60° (см. на рисунке), то углы в основании треугольника ОВА = 180°-60°=120°, и равны между собой: 60° и 60°.
Если в данном по условию треугольнике АВС ∠В=90°, ∠А=60°, то ∠С=180°-90°-60°=30°
Ответ: меньший угол в данном прямоугольном треугольнике = 30°.
Прилагаю чертеж, на котором, использованные выше обозначения.