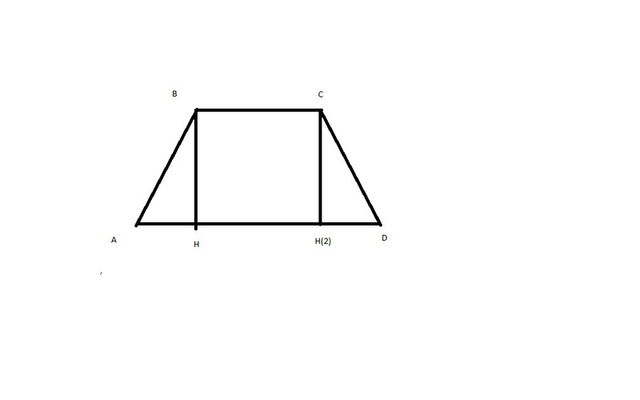
BC - первое основание
AD - второе основание
AB и CD - боковые стороны
H - высота
S(тр) - площадь трапеции
Решение:
S(тр) = (BC+AD)\2 * h = (8 + 14)\2 * 4 = 22\2 * 4 = 44 см²
P(тр) = AB+BC+CD+AD
Т.к. трапеция равнобедренная, то AB = CD
Чертёж, который у вас есть, необходимо будет достроить(вторую высоту начертить)
H(2) - вторая высота
В таком случае, в центре трапеции у вас будет прямоугольник, а по бокам - треугольники
Фигура HBCH(2) - прямоугольник, в котором сторона HH(2) = BC = 8
Можем найти стороны AH и HD.
AH = H(2)D, AD = 14, HH(2) = 8, значит AH = 3 и H(2)D = 3
Рассмотрим треугольник ABH, AB - гипотенуза, AH и BH - катеты
По теореме Пифагора
AB² = AH² + BH²
AB² = 3² + 6²
AB² = 9 + 36
AB² = 45
AB = √45
AB = CD, значит CD = √45
P = 8 + 14 + √45 + √45 = 22 + 3√5 + 3√5 = 22 + 6√5