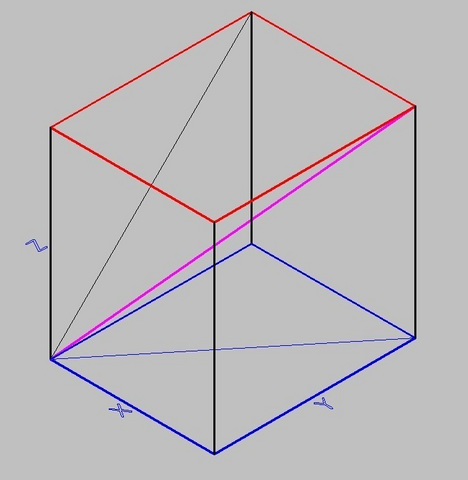
Пусть рёбра параллелепипеда имеют длину x, y, z
длина диагонали
l² = x²+y²+z²
Если угол между диагональю и плоскостью 0xy равен 45°, то
√(x²+y²)/l = cos(45°) = 1/√2
2x²+2y² = l²
x²+y² = z²
Если угол между диагональю и плоскостью 0yz равен 30°, то
√(y²+z²)/l = cos(30°) = √3/2
y²+z² = 3/4*l²
4y²+4z² =3l²
y²+z² = 3x²
---
подставим
y²+x²+y² = 3x²
y = x
x²+y² = z²
2x² = z²
z = x√2
l² = x²+x²+2x² = 4x²
x = l/2
y = l/2
z = l/√2
V = l³/(4√2)