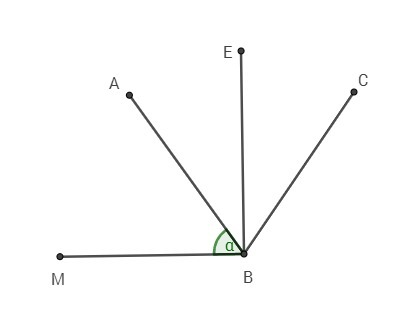
8 (рисунок в приложении)
Пусть дан ∠АВС
ВЕ - биссектриса ∠АВС
ВМ ⊥ ВЕ
∠АВМ = α
Найти: ∠АВС
∠АВЕ = 90° - α (так как ВМ ⊥ ВЕ)
∠АВС = 2*∠АВЕ = 2(90°-α) = 180° - 2α (так как ВЕ - биссектриса ∠АВС)
Ответ: 180° - 2α
9
Пусть AD = СВ = х, тогда:
АС = АВ - х
DВ = АВ - х
Следовательно, АС = DВ, что и требовалось доказать.