Найти площадь фигуры ограниченной графиком функции f:R->R, f(x)= x^2 - 2x +1 и графиком...

РЕШЕНИЕ
F(x) = x² - 2x +1 - функция
F'(x) = 2*x - 2 - производная функции
Площадь - разность интегралов функции - интеграл разности функции.
Находим пределы интегрирования решив уравнение:
x²-2x+1 = 2x-2
Упростили
S = x² - 4x + 3 = 0 - это разность функции!!! - для интегрирования.
Решили квадратное уравнение.
a = 3, b = 1
находим интеграл
$S= \int\limits^3_1 {(x^2-4x+3)} \, dx = \frac{x^3}{3}- \frac{4x^2}{2}+3x$
Вычисляем на границах интегрирования
S(3) = 9 - 18 + 9 = 0 и S(1) = 1/3 - 2 + 3 = 1 1/3
ОТВЕТ : Площадь равна 1 1/3.
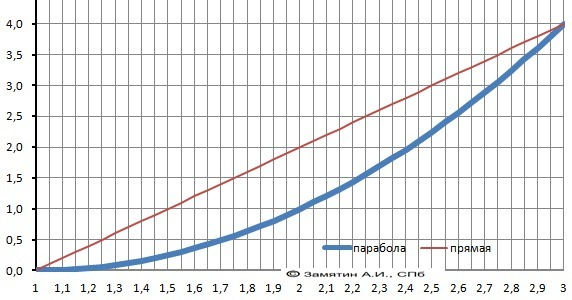
Рисунок с графиками - в приложении.