** стороне AD и диагонали AC параллелограмма ABCD взяты точки E и F соответственно так,...

Question

На стороне AD и диагонали AC параллелограмма ABCD взяты точки E и F соответственно так, что AC=3AF и AD=4AE. Прямая EF пересекает сторону BC в точке G. Найдите площадь параллелограмма, если площадь четырехугольника ABGF равна 10.

Answer 1

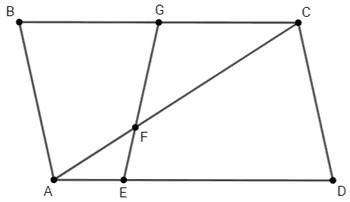
Диагональ делит параллелограмм пополам.
S(ABC)=S(CAD) =S(ABCD)/2

Площади треугольников с равным углом относятся как произведения сторон, содержащих угол.
AC=3AF, AD=4AE
S(FAE)/S(CAD) =AF*AE/AC*AD =1/12 <=>
S(FAE)= S(CAD)/12 =S(ABC)/12

△FAE~△FCG (углы при основаниях равны как накрест лежащие при AD||BC)
AF/CF =1/2
Площади подобных треугольников относятся как квадрат коэффициента подобия.
S(FAE)/S(FCG) =1/4 <=>
S(FCG)= 4S(FAE) =S(ABC)/3

S(ABGF)= 2S(ABC)/3 =S(ABCD)/3 <=>
S(ABCD)= 3S(ABGF) =30

---