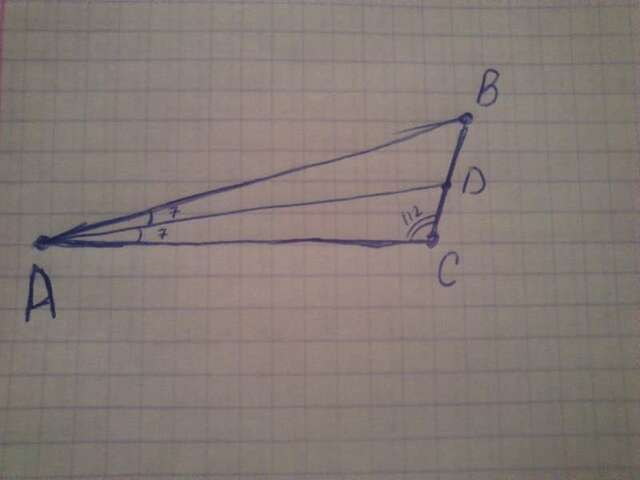
дано :
ABC - треугольник
∠С=112°
AD- биссектриса
∠CAD = 7°
∠B - ?
РЕШЕНИЕ :
в треугольнике ADC:
∠CAD = 7° , AD- биссектриса⇒ ∠ DAB = 7°
т.к. сумма углов в треугольнике = 180° то
∠ADC = 180 - (∠DAC+∠ACD)= 180-(7+112)=61°
по свойству смежных углов углы ∠ADC и ∠ADB в сумме дают 180° ⇒
∠ADB = 180°- ∠ADC=180°-61°=119°
теперь в треугольнике ADB :
∠ B = 180°-(∠ADB+∠BAD)= 180°-(7°+119°)=54°