В треугольнике ABC биссектрисы углов A и C пересекаются в точке L. Через точку L...

Question

В треугольнике ABC биссектрисы углов A и C пересекаются в точке L. Через точку L проведена прямая MK параллейна AC ( точка M лежит на стороне AB , а точка K- на стороне BC ) . Найдите сумму AM и KC, если MK 13 см

Answer 1

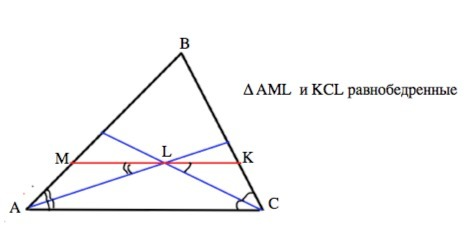
Параллельные прямые МК и АС при их пересечении секущей АL  образуют равные накрестлежащие углы МLА и LAC. 

Но ∠МАL=∠LAC ( АL – биссектриса). 

Следовательно, в ∆ АМL  углы при основании AL равны. ⇒ 

∆ АМL  равнобедренный. АМ=ML. 

Аналогично доказывается равенство KL=KC в ∆ СКL ⇒

АМ+КС=МL+КL=13 см.

---