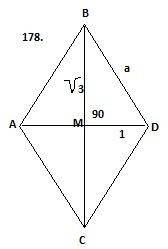
178. Зная, что диагонали ромба пересекаются под углом 90° и в точке пересечения диагонали делятся пополам, найдем сторону ромба:
а=√((D/2)²+(d/2)²)=√(3+1)=2
Углы найдем по теореме синусов:
MD/sin1/2B=BD/sin90°, sin1/2B=MD*sin90/BD, sin1/2B=1/2⇒1/2B=30°⇒∠B=∠C=60°
∠B=∠C=(360-2*60)/2=120°
Ответ:120°,120°,60°,60°.
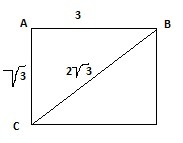
179. Диагональ найдем по теореме Пифагора:
√(3²+(√3)²)=√12=2√3
Снова воспользуемся теоремой синусов
D/sin90=3/sinC⇒sinC=3*sin90/(2√3)=√3/2⇒∠C=60°⇒∠B=90-60=30°
Ответ:30°,60°