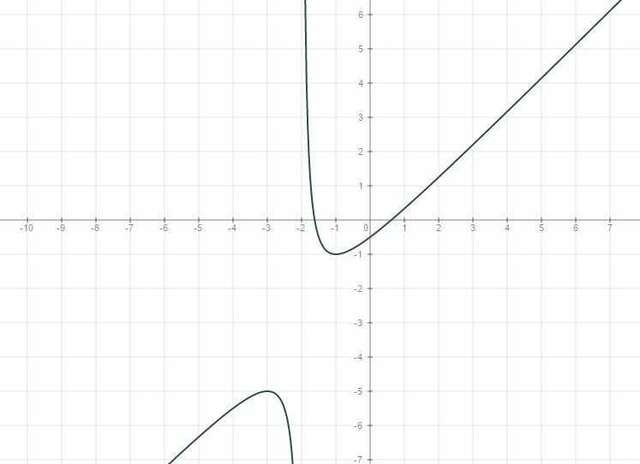
Y=(x²+x-1)/(x+2) x≠-2 вертик. асимптота
x=0 y=-1/2
x²+x-1=0 D=1+4=5 x1=1/2[-1-√5]=-0.5-√5/2
x2=1/2[-1+√5]=-0.5+√5/2
y'=(u/v)'=[u'v-v'u]/v² u=x²+x-1 u'=2x+1 v=x+2 v'=1
y'=[(2x+1)(x+2)-(x²+x-1)]/(x+2)²
(2x+1)(x+2)-(x²+x-1)=2x²+x+4x+2-x²-x+1=x²+4x+3 x1=-1 x2=-3
--------------------- -3--------------------- -1---------------------
+ - +
функция возрастает х∈(-∞,-3)∪(1,∞)
убывает ·х∈(-3,-2)∪(-2,-1) макс при х=-3 миним. при х=-1