Формула суммы углов выпуклого многоугольника
N=180°•(n-2), где N- сумма углов многоугольника, n - количество его сторон.
Сумма углов треугольника 180°, пятиугольника –180•3.
Сложим суммы углов пяти треугольников, расположенных на сторонах пятиугольника, сумму углов пятиугольника и сумму равных им вертикальных углов при вершинах пятиугольника .
180°•5+180°•3+180°•3=180°•11
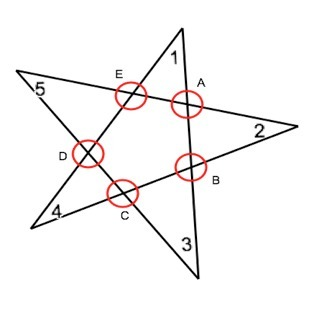
Вычтем из этой суммы суммы углов, образованных пересечением сторон звезды. Каждый из них равен 360°, или 180°•2. Т.к.их 5, всего нужно вычесть 180°•10 (см. рисунок).
Получим 180°•11-180°•10=180°