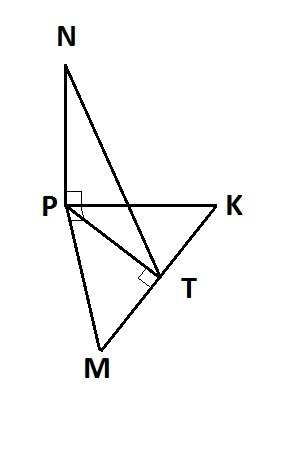
Треугольник MPK равнобедренный, P = 90°. Значит, углы M и K равны 45°.
NT - расстояние от точки N до гипотенузы MK. Так как PN ⊥ MPK, T - середина MK.
Из треугольника MPK по т.Пифагора
MK = √(MP²+PK²) = √(100+100) = √(200) = 2√(50)
Так как T - середина MK,
MT = TK = √(50)
Рассмотрим треугольник MPT. Угол M = 45° по условию. Угол MPT = половине угла MPK, т.к. PT - высота и биссектриса треугольника MPK
∠MPT = 90°:2 = 45°
Треугольник MPT - равнобедренный, MT = PT = √(50)
Тогда из треугольника NPT по т.Пифагора
NT = √(PN²+PT²) = √(31+50) = √(81) = 9 см.