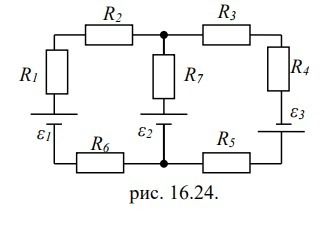
В схеме, изображенной ** рис. 16.24, ε1=10,0В, ε2=20,0 В, ε3=30,0В, R1=1,0 Ом, R2=2,0 Ом,...

Question

259 просмотров

В схеме, изображенной на рис. 16.24, ε1=10,0В, ε2=20,0 В,
ε3=30,0В, R1=1,0 Ом, R2=2,0 Ом, R3= 3,0 Ом, R4=4,0 Ом, R5=5,0 Ом,
R6=6,0 Ом и R7=7,0 Ом. Внутреннее сопротивление источников
пренебрежимо мало. Определите: 1) величины токов во всех участках цепи; 2) работу, совершенную вторым источником за промежуток
времени Δt=0,1 с.
Ответ: I1= 0,6 А, I2= 2,2 А, I3= 2,8 А, А2=4,4 Дж

Физика nuzhakov_zn (202 баллов) 27 Май, 18 | 259 просмотров

Дан 1 ответ

Правильный ответ

Воспользуемся методом контурных токов. Выделим два независимых контура. Первый образован элементами R₁, R₂, R₇, E₂, R₆, E₁, второй - элементами R₃, R₄, E₃, R₅, E₂, R₇.
Направим в каждом контуре контурные токи I₁₁ и I₂₂ по часовой стрелке. Токи, протекающие через источники, направим от плюса к минусу.
Для каждого контура запишем уравнение по второму закону Кирхгофа
$\displaystyle \left \{ {{I_{11}(R_1+R_2+R_7+R_6)-I_{22}\cdot R_7=E_2-E_1} \atop {-I_{11}\cdot R_7+I_{22}(R_3+R_4+R_5+R_7)=-E_3-E_2}} \right.$
Подставляем числовые данные
$\displaystyle \left \{ {{I_{11}(1+2+7+6)-I_{22}\cdot 7=20-10} \atop {-I_{11}\cdot 7+I_{22}(3+4+5+7)=-30-20}} \right. \\ \\ \\ \left \{ {{16\cdot I_{11}-7\cdot I_{22}=10} \atop {-7\cdot I_{11}+19\cdot I_{22}=-50}} \right.$
Решаем полученную систему уравнений по правилу Крамера.
$\displaystyle \Delta=255; \quad \Delta_{11}=-160; \quad \Delta_{22}=-730 \\ \\ I_{11}= -\frac{160}{255}= -\frac{32}{51}\approx -0.63 \\ \\ I_{22}=- \frac{730}{255}=- \frac{146}{51}\approx -2.86 \\ \\ I_1=0.63, \quad I_3=2.86, \quad I_2=I_3-I_1=2.23 \\ \\ A_2=E_2I_2\cdot0.1=20\cdot2.23\cdot0.1\approx4.46$

Эникей_zn (150k баллов) 27 Май, 18