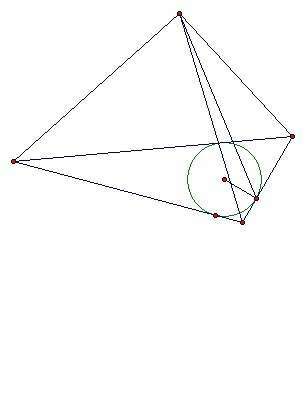
Если двугранные углы при основании пирамиды равны, то будут равны высоты боковых граней, а высота пирамиды приходит в центр вписанной окружности основания. Проекции высот боковых граней - радиусы вписанной окружности для основания. В прямоугольном треугольнике радиус вписанной окружности вычисляется по формуле r=(a+b-c)/2.
c=√(6²+8²) = 10.
r=(6+8-10)/2 = 2. Высоты боковых граней находим по теореме Пифагора.
h=√(2²+(√21)²= √25 = 5.
S(бок) = 1/2*6*5 + 1/2*8*5 + 1/2*10*5 = 1/2*5*(6+8+10) = 60 см².