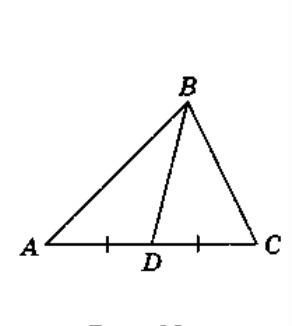
Нехай у трикутнику ABC АВ = 9 см, ВС = 7 см, AD = DC , BD = 4 см. Із трикутника ABD маємо:
АВ^(2)= AD^(2)+BD^(2)–2AD∙BD∙
cosкутаADB
81=AD^(2)+16-2AD·4·cosкутаADB (1)
Із трикутника BDC маємо:
ВС^(2) = DC^(2) + BD^(2) – 2DC ∙ BD ∙cosBDC
BC2 = AD^(2) + BD^(2) – 2AD ∙ BD ∙ cos(180° - кутADB)
BC^(2) = AD^(2) + BD^(2) + 2AD ∙ BD ∙ cosкутADB
49=AD^(2)+16+8AD cosкутаADB (2)
Додавши почленно рівності (1) і (2), маємо: 49 + 11 = 2AD^(2) + 32, 2AD^(2) = 98 , AD2 = 49, звідси AD = 7 (см).
Відповідь. 7 см.