Половина высоты относится к радиусу вписанной окружности основания как tg(a)
tg(a) = h/2/r
r = h/(2tg(a))
В равностороннем треугольнике центр вписанной окружности - это точка пересечения медиан, биссектрис и высот. Медианы делятся точкой пересечения как 2 к 1 начиная от угла, и которого построена медиана. Поэтому полная длина медианы равна 3r
Рассмотрим прямоугольный треугольник, равный половине основания. Обозначим сторону основания x. Тогда по Пифагору
x² = (x/2)² + (3r)²
3/4*x² = 9r²
x² = 12r²
x = 2√3*r = 2√3*h/(2tg(a)) = h√3/tg(a)
Площадь основания
S = 1/2*x*3r = 1/2*h√3/tg(a)*h/(2tg(a)) = √3/4*(h/tg(a))²
И объём
V = 1/3*S*h = 1/3*√3/4*(h/tg(a))²*h = 1/(4√3)*h³/(tg(a))²
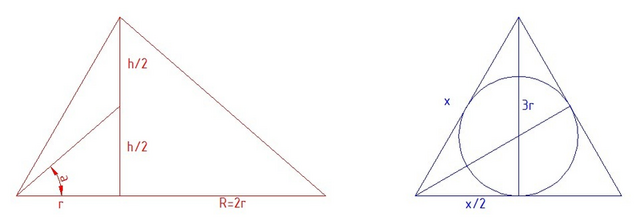
на картинке слева сечение пирамиды в вертикальной плоскости, справа - основание.