Задачи по теории вероятности лучше решать в более общем виде, чтобы на каждом этапе расчета его можно было бы проверить.
Расчет проведен в таблице - в приложении.
РЕШЕНИЕ с пояснениями - лишние слова можно и удалить.
Событие - выбрать СЛУЧАЙНУЮ БРАКОВАННУЮ состоит из двух.
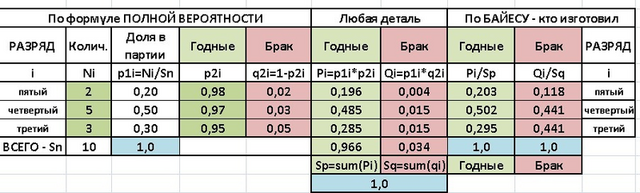
Вероятность деталей в партии - р1(i) - найдем по количеству работников.
p11 = 2/10 = 0,2, аналогично - p21=0,5, p31=0,3.
Вероятность брака - q2(i) - дано. Для общности найдем вероятность годной детали у каждого работника.
p21=1-q11 = 0,98, p22=0,97, p23 = 0,95.
ГЛАВНОЕ: Вероятность нашего события - "выбрать И случайную И бракованную ИЛИ 5р ИЛИ 4р ИЛИ 3р равна СУММЕ ПРОИЗВЕДЕНИЙ вероятности каждого из возможных.
Заполняем столбики - любая годная и любая бракованная и находим сумму произведений.
Sq = 0,2*0,02 + 0,5*0,03 + 0,3*0,05 = 0,004+0,015+0,15=0,034= 3,4% - случайная бракованная - ОТВЕТ
Не трудно найти и вероятность случайной годной - Sp =0,966=96,6%.
Проверяем - сумма вероятностей равна 1.
ДОПОЛНИТЕЛЬНО
По формуле Байеса можно посчитать, что эту бракованную деталь с равной вероятностью 44,1% могли сделать и 4 и 3р.
А вот годную - с вероятностью 50,2% - четвертый разряд.