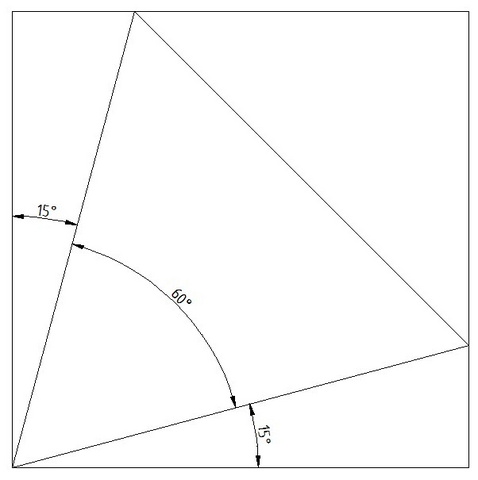
Внутри прямого угла квадрата, 90 градусов, симметрично расположен угол треугольника 60 градусов. Нижняя сторона квадрата, отрезок правой стороны квадрата и сторона треугольника образуют прямоугольный треугольник.
Нас интересует его гипотенуза. Обозначим сторону квадрата a
10/a = cos(15°)
Для того, чтобы получить решение в радикалах, а не в непонятных arccos(15) воспользуемся формулами половинного угла
cos²(α/2) = (1+cos(α))/2
cos(15°) = √(1/2+cos(30°)/2) = √(1/2+√3/4) = 1/4(√2+√6)
a = 10/cos(15°) = 10/(1/4(√2+√6)) = 10(√6-√2) см
И площадь треугольника
S = 1/2*a²*sin(60°) = 1/2*(10(√6-√2))²*√3/2 = 200√3-300 см²