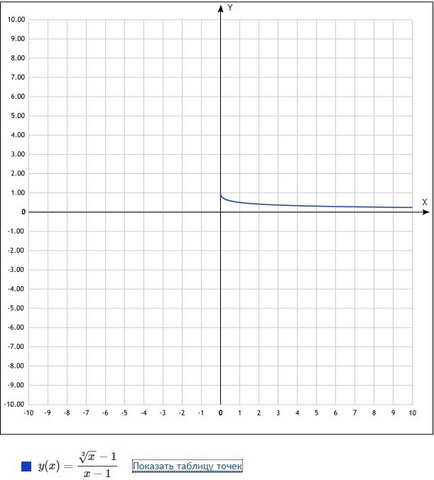
f(p)=(√p-1)/(p-1)
f`(p)=(0.5(p-1)-(√p-1))/(√p(p-1)^2)=(-0.5-0.5p+√p)/(√p(p-1)^2)=-(√p-1)^2/(2√p(p-1)^2)=
-1/(2√p(√p-1)^2)
в числителе производной -1, ее приравнять к 0 нельзя, это говорит о том, что у функции нет экстремальных точек
т.к. производная отрицательна, значит функция убывает, значит максимально значение надо искать справа на границе ОДЗ
ОДЗ для f(p): р>=0; p не равен 1
Учитывая все это максимальное значение f(p) будет при р=0
f(0)=(√0-1)/(0-1)=-1/-1=1