№10
Дано: Δ АВС
∠А:∠В:∠С = 1:2:3
Найти:вид Δ АВС
Решение.
Сумма углов треугольника
180°.
Если
∠А = х, то из заданного отношения
∠В = 2х и ∠С = 3х
∠А + ∠В + ∠С = х + 2х + 3х = 180°
6х = 180°
х = 180 : 6 = 30°
Отсюда :
∠А = 30° ; ∠В = 2*30 = 60°; ∠С = 3*30 = 90°, т.е.
Δ АВС - прямоугольный
Ответ:
с). Прямоугольный
№ 11.
Дано: Δ АВС
∠С > ∠А + ∠В
Найти:вид Δ АВС
Решение.
Сумма углов треугольника
180°.
∠А + ∠В + ∠С = 180°, отсюда
(∠А + ∠В) = 180° - ∠С
По условию
∠ С > (∠A + ∠B), т.е
∠С > 180° - ∠С ⇒
2∠С > 180° ⇒
∠С > 90°.
Значит, ΔАВС - тупоугольный.
Ответ:
d). Тупоугольный
№ 12
Дано:
Δ АВС
∠С = 90°
∠А : ∠В = 1 : 2
Найти: ∠В
Решение:
Сумма углов треугольника
180°. ⇒
∠А + ∠В = 180° - ∠С = 180° - 90° = 90°
Если
∠А = х, то
∠В = 2х, тогда
∠А + ∠В = х+2х=90°;
3Х = 90°
х = 30° , это
∠А
∠В = 2*30 = 60°
Ответ:
с). 60°
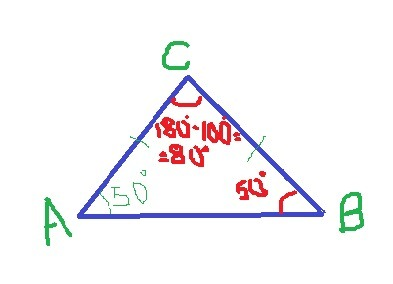
№ 13.
Дано: Δ АВС
∠А = 50°
АС = ВС
Найти: ∠С
Решение.
Из условия следует, что Δ АВС - равнобедренный с вершиной С, а
∠А = ∠В как углы при основании равнобедренно треугольника, т.е.
∠В = 50° (см. рисунок)
Сумма углов треугольника
180°
∠С = 180° - ∠А - ∠В = 180° - 50° - 50° = 80°
Ответ: d). 80°