Найти площадь фигуры ограниченной графиком функции y=x^2-6x+5 и осью Ox

ДУМАЕМ
Площадь - интеграл разности функций.
ДАНО
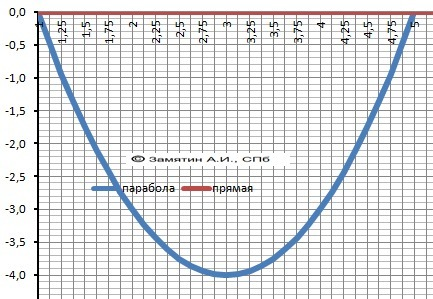
Y₁ = 0
Y₂ = x² - 6*x + 5
РЕШЕНИЕ
Находим пределы интегрирования - общие точки.
Решаем уравнение
Y₂ = x² - 6*x + 5 = Y₁ = 0
Корни уравнения: a = 5, b = 1
Находим интеграл разности
$S= \int\limits^5_1 (-5+6*x-x^2)} \, dx= - \frac{5x}{1}+ \frac{6x^2}{2}- \frac{x^3}{3}$
Вычисляем при а = 5
S(5) = -25 + 75 - 41 2/3 = 8 1/3
S(1) = - 5 +3 - 1/3 = - 2 1/3
Вычисляем разность и находим ответ.
S = 8 1/3 - (-2 1/3) = 10 2/3 ≈ 10.667 - ОТВЕТ