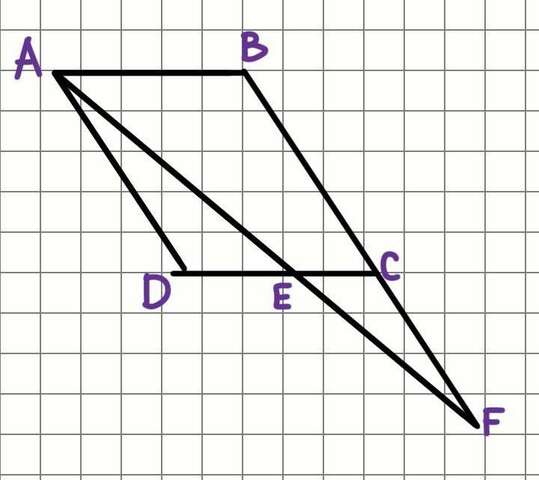
AB и DC параллельны (противоположные стороны параллелограмма).
∠BAF = ∠CEF - соответствующие углы при AB║CD и секущей AF.
∠ABC = ∠ECF - соответствующие углы при AB║CD и секущей BF.
Рассмотрим ΔABF и ΔECF
1. ∠BAF = ∠CEF (из решения)
2. ∠ABC = ∠ECF (из решения)
Отсюда следует, что ΔABF и ΔECF подобны по трём углам.
Найдём коэффициент подобия, он равен отношению подобных сторон треугольников:
k = BC/BF = 56/(56+30) = 56/86 = 28/43
Также из подобия следует, что EC:AB = k
Найдём AB из этой записи:
15/AB = 28/43
AB = 15*43/28
AB = 645/28
AB = CD = 645/28 (так как ABCD параллелограмм)
DE = DC - EC = 645/28 - 15 = (645-420)/28 = 25/28
Ответ: 25/28