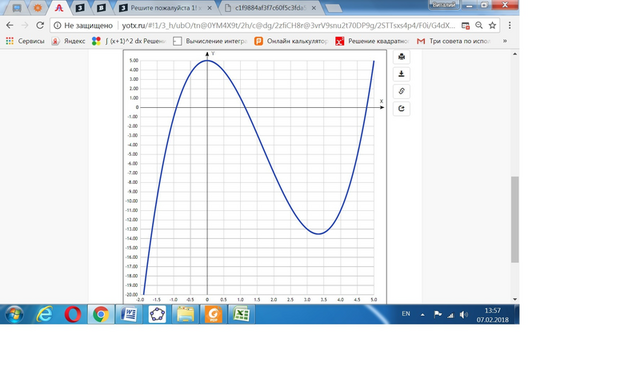
Дана функция х³ - 5х² + 5. Найти уmax, ymin.
Для этого надо найти производную и приравнять её нулю.
y' = 3x² - 10x = 0.
x(3x - 10) = 0.
Получаем 2 критические точки х = 0 и х = (10/3) и 3 промежутка монотонности функции: (-∞; 0), (0; (10/3)) и ((10/3); +∞).
На
промежутках находят знаки производной. Где
производная положительна - функция возрастает, где отрицательна - там убывает.
Точки, в которых происходит смена знака и есть точки экстремума - где
производная с плюса меняется на минус - точка максимума, а где с минуса на плюс
- точки минимума.
x =
-1
0
1
3,3333 4
y' = 13
0 -7
0 8.
Как видим:
хmax = 0, уmax = 0-5*0+5 = 5.
хmin = (10/3), уmin = (10/3)³ - 5*(10/3)² + 5 = (1000/27) - (500/9) + 5 = -13,5185.
На заданном отрезке максимум функции равен 5 при х = 0.
Для минимума надо подставить значения х = 1 и х = -1 в уравнение функции:
х = 1, у = 1-5+5 = 1,
х =-1, у = -1-5+5 = -1 это минимум.