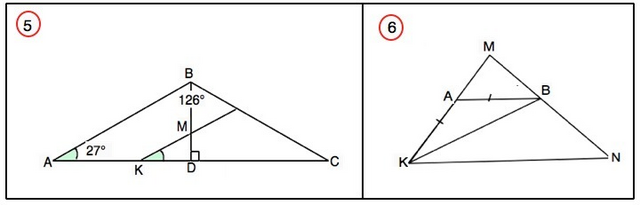
№5. Треугольник АВС – равнобедренный с основанием АС. На его биссектрисе ВD взята точка М, а на основании – точка К, причем МК||АВ. Найдите углы треугольника МКD, если угол АВС=126°, угол ВАС=27°
МК ║ АВ При пересечении параллельных прямых секущей соответственные углы равны. ⇒
∠МКD=∠ВАС=27°
Биссектриса равнобедренного треугольника, проведенная между равными сторонами, является его высотой. Следовательно, ∠ BDK=90°
∠КМD=180°-90°-27°=53°
Углы ∆ МКD равны 27°, 90°, 53° (Величина угла АВС для решения оказалась лишней).
---------------
№6. Докажите, что на рисунке прямые АВ и KN параллельны, если треугольник АВК –равнобедренный с основанием ВК, а луч КВ является биссектрисой угла АКN. , что на рисунке прямые АВ и КN (См. рисунок)
По свойству углов при основании равнобедренного треугольника ∠АВК=∠ВКА.
Так как КВ - биссектриса, то ∠АКВ=∠ВКN.
Но угол АКВ=АВК. ⇒
Накрестлежащие углы АВК и ВКN равны.
Равенство накрестлежащих углов при пересечении двух прямых секущей - признак параллельности этих прямых. ⇒
АВ║KN, ч.т.д.