Найти наибольшее и наименьшее значение на отрезке f(x)=x^5-5x^4+5x^3+1 ; [-2;2]

ДАНО
y(x) = x⁵ - 5x⁴ + 5x³ + 1
РЕШЕНИЕ
Находим экстремумы функции - корни производной.
y'(x) = 5x⁴ - 20x³ + 15x² = 5x²*(x² - 4x + 3) = 5*x²*(x-1)(x-3)
Корни = x₁= 0, x₂ =1 и x₃ =3 (вне интервала)
Вычисляем значения экстремумов внутри интервала.
y(0) = 1
y(1) = 2 - максимальное значение.
Функция возрастающая - минимум на левой границе области определения.
у(-2) = -2⁵ - 5*2⁴ - 5*2³ + 1 = - 32 - 80 - 40 + 1 = - 151 - минимум
ОТВЕТ: Е(у)∈(-151;2)
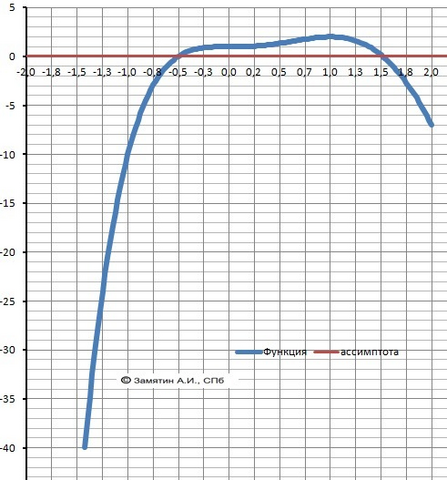
График функции - в приложении - в подарок.
Минимум = - 151 - за пределами рисунка. Зато видны экстремумы при 0 и 1.

Найти наибольшее и наименьшее значение ** отрезке f(x)=x^5-5x^4+5x^3+1 ; [-2;2]