5 блок 1 задача
параллелограмм АВСD, АВ=СD, АД=ВС, проводим высоту ВК на СD, площадь АВСD=СD*ВК, М - произвольная точка (для построения - если считать точку О пересечение диагоналей то М по диагонали АС между А и О , ближе к О), через точку М проводим линию параллельную ВК, на АВ она пересекается в точке К, на продолжении СD в точке Т,КМ-высота для треугольника АВМ, площадь треугольника АВМ=1/2*АВ(СD)*МК,МТ-высота для треугольника СМD, площадь СМD=1/2*СD(АВ)*МТ, площадь АВМ+площадь СМD=1/2*СD*МК+1/2*СD*МТ=1/2 СD*(МК+МТ), но МК+МТ=КТ, а КТ=ВК, тогда площадь АВМ+площадь СМD=1/2*СD*ВК, т.е=1/2 площади ABCD
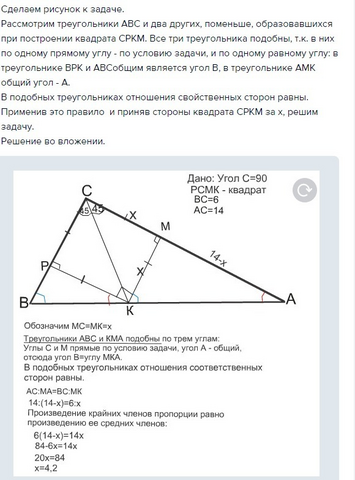
2 задача на рисунке