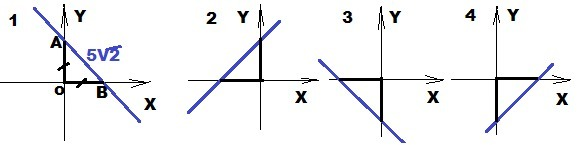
Данное решение для первой четверти. Для остальных четвертей решение аналогичное
AB = 5√2; OA = OB - по условию
ΔOAB - прямоугольный равнобедренный
Теорема Пифагора
OA² + OB² = AB² ⇒ 2OA² = AB²
2OA² = (5√2)²
2OA² = 50 ⇒ OA² = 25 ⇒ OA = OB = 5
Координаты точек А (0; 5), В (5; 0)
Уравнение прямой y = kx+b
Для точки А: 5 = k*0 + b; b = 5
Для точки В: 0 = k*5 + b; 5k = -b; k = -b/5;
k = -5/5 = -1
Уравнение прямой для первой четверти y = -x + 5
Уравнение прямой для второй четверти y = x + 5
Уравнение прямой для третьей четверти y = -x - 5
Уравнение прямой для четвертой четверти y = x - 5