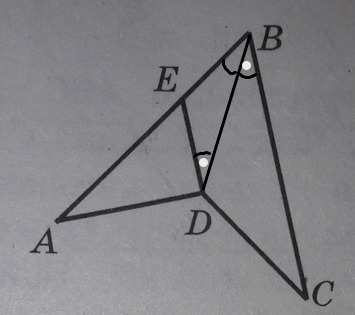
Дано: AB=BC, AD=DC, BE=ED. Доказать: BC параллельно DE.

Проведем отрезок ВD ∆ ABD~∆ CBD по трём сторонам.--

∠АВD=∠CBD

∆ ВЕD равнобедренный ( BE=ED). Следовательно, ∠DBE=∠EDB.

Из доказанного выше ∠DBE=∠BDE. Эти углы накрестлежащие при пересечении ED и BC секущей BD.

Равенство накрестлежащих углов при пересечении двух прямых секущей - признак параллельности этих прямых. ⇒

ВС║DE. Доказано.