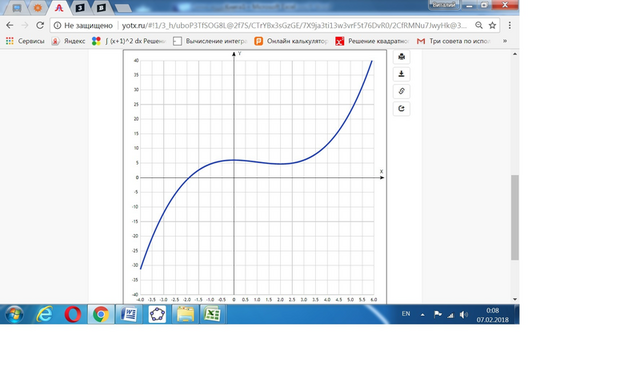
Дана функция у = (1/3)x³-x²+6.
1) Производная равна y' = x² - 2x.
Приравняем её нулю: x² - 2x = 0,
х(х - 2) = 0.
Получаем 2 критические точки и 3 промежутка монотонности функции.
На
промежутках находим знаки производной. Где
производная положительна - функция возрастает, где отрицательна - там убывает.
Точки, в которых происходит смена знака и есть точки экстремума - где
производная с плюса меняется на минус - точка максимума, а где с минуса на плюс
- точки минимума.
x =
-1
0 1 2 3
y' =
3 0
-1 0 3.
Как видим, в точке х = 2 минимум функции,
у = (1/3)*2³ - 2² + 6 = 14/3 = 4(2/3)
в точке х = 0 максимум функции,
у = 6.
2) Промежуток убывания один: (0; 2).
3) Находим вторую производную: y'' = 2x - 2.
Приравняем нулю: 2(х - 1) = 0.
Имеем 1 точку перегиба х = 1.
у = (1/3)-1+6 = 5(1/3).
4) Где
вторая производная меньше нуля, там график функции выпуклый, а где больше -
вогнутый.
x = 0
1
2
y'' = -2
0 2.
График выпуклый вверх на промежутке (-∞; 1).
5) График в приложении.