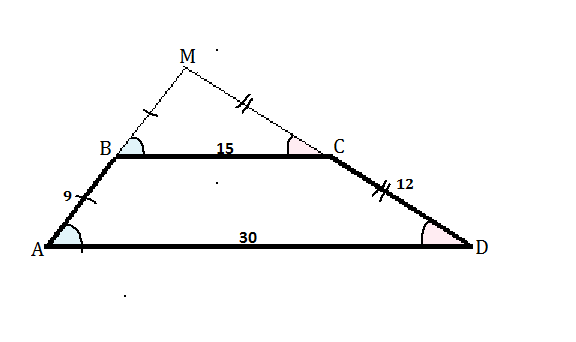
Пусть дана трапеция АВСD, а продолжения ее сторон пересекаются в точке М.
Тогда треугольники АМD и ВМС подобны, т.к. ВС - параллельна АD как сторона трапеции, углы при основаниях ВС и АD соответственно равны как углы при пересечении параллельных прямых секущими.
В треугольнике АМD отношение АD:ВС=2:1, и ВС является средней линией треугольника АМD.
⇒
МВ=АВ=9,
МС=СD=12.
Отношение сторон в треугольнике ВМС равно отношению сторон в треугольнике АМД:
ВМ:МС:ВС=9:12:15=3:4:5- это отношение сторон египетского треугольника. ⇒
Δ ВМС прямоугольный, угол ВМС=90°
Убедимся в этом, проверив по т.Пифагора:
ВС²=ВМ²+МС²
225=81+144
Угол, который образуют продолжения боковых сторон трапеции, равен 90°
-------
Угол АМС пожно найти и по т. косинусов, если Вы ее уже изучали. Получим косинус ∠ АМD=0, и это косинус 90°