Формула объёма пирамиды
V=S•H:3
где S - площадь основания (трапеции) и, Н - высоту пирамиды, нужно найти.
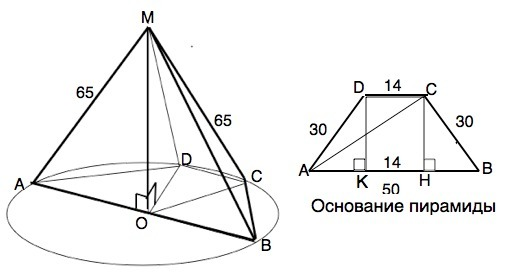
Обозначим пирамиду МАВСD.
МО - высота пирамиды. AB║CD, CD=14 см, AB=50 см, AD=BC=30 см
Ребра пирамиды - равные по условию наклонные с вершиной в т.М, следовательно, их проекции также равны, и равны они радиусу описанной около основания окружности.
Для нахождения площади основания нужно найти высоту трапеции АВСD.
Опустим из тупых углов трапеции высоты DK и СН. Они делят трапецию на два равных прямоугольных треугольника, гипотенузой которых является боковые стороны, и прямоугольник DCHK
АК=ВН=(АВ-СD):2=18 см
Из ∆ СНВ по т.Пифагора высота трапеции
СН=√(BC²-BH²)=√(900-324)=24 см
S (АВСD)=CH•(AB+CD):2=24•(50+14)²2=768 см²
Для нахождения высоты трапеции найдём проекции ребер, т.е. радиус описанной около основания окружности.
Проведем в трапеции диагональ АС.
Из ∆ АСН по т. Пифагора АС=√(AH²+CH²)=√(32²+24²)=40 см
Окружность описана около трапеции, следовательно, она описана около треугольникоа АВС и АСD, т.к. их вершины лежат на окружности.
Радиус описанной около треугольника окружности
(a,b,c - стороны треугольника, 4S- его учетверенная площадь
Площадь ∆ АDC по известной ф.Герона равна 168 см² ⇒
см.
Диаметр окружности 2•25=50 см, ⇒ большее основание трапеции – диаметр описанной около нее окружности, и вершина М пирамиды проецируется в её центр О.
Из прямоугольного ∆ МОВ по т.Пифагора
МО=√(MB²-BO²)=√(65²-25²)=60 см.
V=768•60:3=15360 см³
