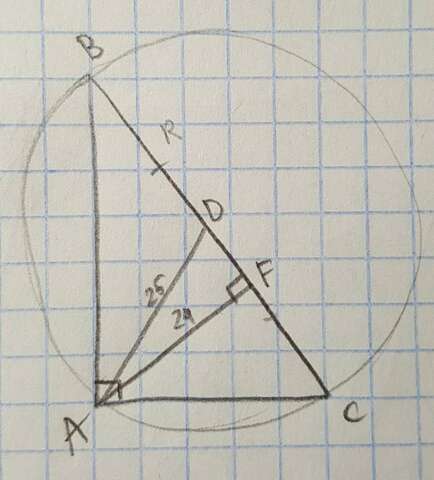
По теореме медиана проведенная из вершины прямого угла равна половине гипотенузы.
AD=0.5BC
отсюда ВС=50.
описываем вокруг тр.АВС окружность.
т.к. он прямоугольный, то ВС-диаметр(угол в 90 гр. опирается на дугу в 180 гр.)
значит BD и DC-радиусы (AD-медиана)
рассмотрим тр.ADF (прямоугольный т.к. AF-высота)
находим DF по т.Пифагора
DF^2=AD^2-AF^2
DF^2=625-576=49
DF=7
рассмотрим тр. AFC
FC=DC-DF
FC=25-7=18
находим АС по т.Пифагора
АС^2=FC^2+AF^2
AC^2=324+576=900
AC=30
рассмотрим тр. ABC
находим по т.Пифагора сторону АВ
АВ^2=BC^2-AC^2
AB^2=2500-900=1600
AB=40
формула площади в прямоугольном тр.
S=AB*AC
S=40*30=1200
периметр:
P=AB+BC+AC
P=40+30+50=120
ответ: 120; 1200.