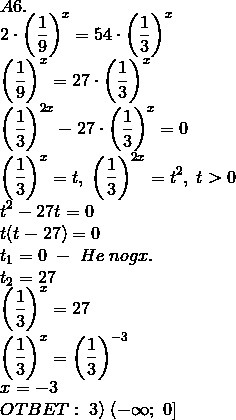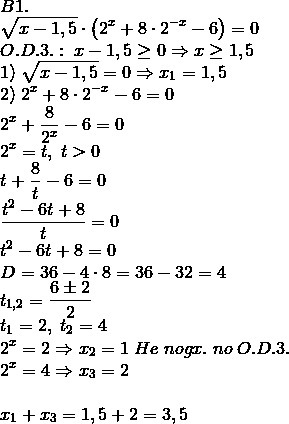0\\t^2-27t=0\\t(t-27)=0\\t_1=0\;-\;He\;nogx.\\t_2=27\\\left(\frac13\right)^x=27\\\left(\frac13\right)^x=\left(\frac13\right)^{-3}\\x=-3\\OTBET:\;3)\;(-\infty;\;0]" alt="A6.\\2\cdot\left(\frac19\right)^x=54\cdot\left(\frac13\right)^x\\\left(\frac19\right)^x=27\cdot\left(\frac13\right)^x\\\left(\frac13\right)^{2x}-27\cdot\left(\frac13\right)^x=0\\\left(\frac13\right)^x=t,\;\left(\frac13\right)^{2x}=t^2,\;t>0\\t^2-27t=0\\t(t-27)=0\\t_1=0\;-\;He\;nogx.\\t_2=27\\\left(\frac13\right)^x=27\\\left(\frac13\right)^x=\left(\frac13\right)^{-3}\\x=-3\\OTBET:\;3)\;(-\infty;\;0]" align="absmiddle" class="latex-formula">

0\\t+\frac8t-6=0\\\frac{t^2-6t+8}t=0\\t^2-6t+8=0\\D=36-4\cdot8=36-32=4\\t_{1,2}=\frac{6\pm2}2\\t_1=2,\;t_2=4\\2^x=2\Rightarrow x_2=1\;He\;nogx.\;no\;O.D.3.\\2^x=4\Rightarrow x_3=2\\\\x_1+x_3=1,5+2=3,5" alt="B1.\\\sqrt{x-1,5}\cdot\left(2^x+8\cdot2^{-x}-6\right)=0\\O.D.3.:\;x-1,5\geq0\Rightarrow x\geq1,5\\1)\;\sqrt{x-1,5}=0\Rightarrow x_1=1,5\\2)\;2^x+8\cdot2^{-x}-6=0\\2^x+\frac8{2^x}-6=0\\2^x=t,\;t>0\\t+\frac8t-6=0\\\frac{t^2-6t+8}t=0\\t^2-6t+8=0\\D=36-4\cdot8=36-32=4\\t_{1,2}=\frac{6\pm2}2\\t_1=2,\;t_2=4\\2^x=2\Rightarrow x_2=1\;He\;nogx.\;no\;O.D.3.\\2^x=4\Rightarrow x_3=2\\\\x_1+x_3=1,5+2=3,5" align="absmiddle" class="latex-formula">