** отрезке AC отмечена точка B. ** отрезках AB, BC и AC, как ** диаметрах, в одной...

Question

На отрезке AC отмечена точка B. На отрезках AB, BC и AC, как на
диаметрах, в одной полуплоскости построены полуокружности. Окружность с цен-
тром в точке O касается все этих полуокружностей (см. рис.). Найдите радиус этой
окружности, если AB = 4, BC = 2.

---

Answer 1

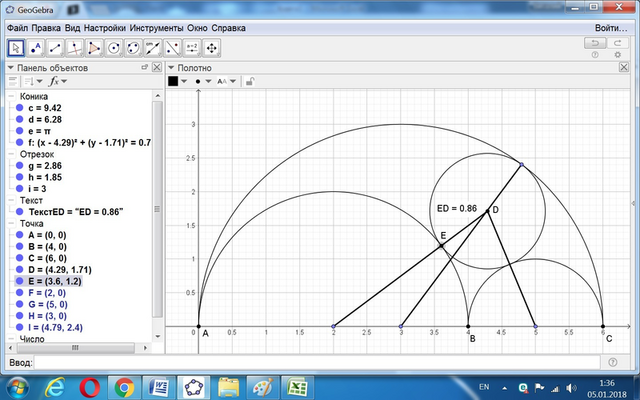
Данный чертёж поместим в прямоугольную систему координат точкой А в начало, АС - по оси Ох.
Координаты центра окружности обозначим (х; у), радиус - R.
Тогда условие касания заданной окружности к исходным полуокружностям можно записать в виде системы из трёх уравнений:
(x-2)^2+y^2=(2+R)^2, (5-x)^2+y^2=(1+R)^2, (3-R)^2=(x-3)^2+y^2.
Решая эту систему, получаем результат:
х = (30/7), у = (12/7) и R = (6/7) ≈ 0,857143.

---