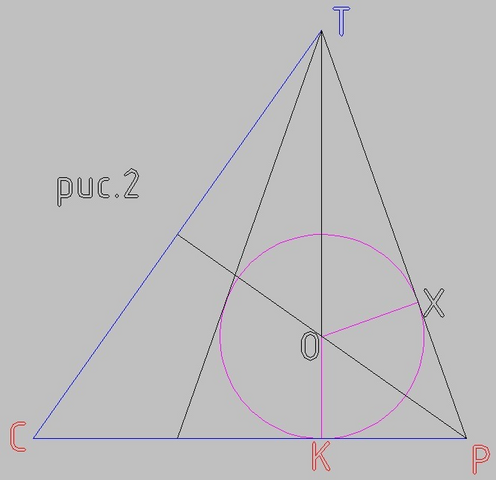
Первый рисунок - вид пирамиды в 3д
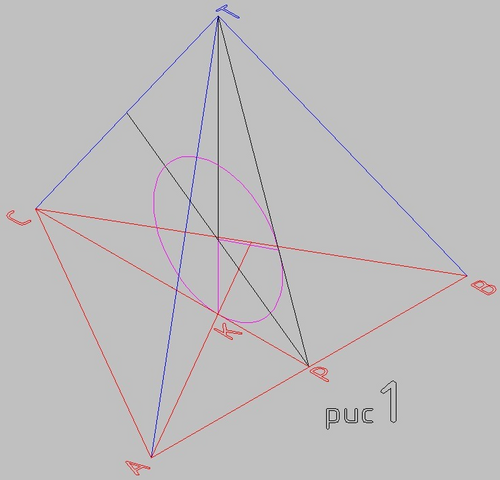
второй рисунок - сечени пирамиды в вертикальной плоскости
ОК = ОХ = r
∠CPT = β
СР - высота, медиана и биссектриса основания
по свойству точки пересечения медиан
СК = 2*КР
СР = 3*КР
------------
если сторона основания а, то высота основания СР по Пифагору
a² = (a/2)² + CP²
CP² = 3/4*a²
CP = a√3/2
Площадь основания
S = 1/2*a*a√3/2 = a²√3/4
KP = CP/3 = a/(2√3)
r/KP = tg(β/2)
KP = r/tg(β/2)
a/(2√3) = r/tg(β/2)
a = √3/2*r/tg(β/2)
S = a²√3/4 = (√3/2*r/tg(β/2))²√3/4 = 3/4*r²/tg²(β/2)*√3/4 = 3√3/16*r²/tg²(β/2)
KP/TK = tg(90-β) =1/tg(β)
h = TK = KP*tg(β) = r*tg(β)/tg(β/2)
V = 1/3*S*h = 1/3 * 3√3/16*r²/tg²(β/2) * r*tg(β)/tg(β/2) = √3/16*r³tg(β)/tg³(β/2)