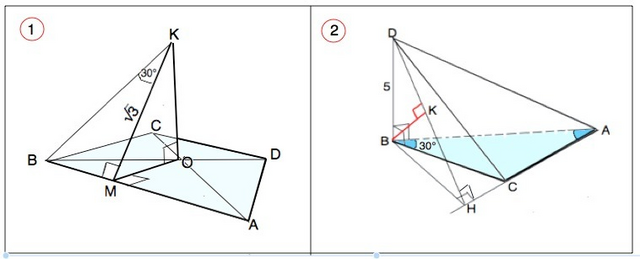
1. a) КО - перпендикуляр к плоскости АВСД.
КМ - наклонная, перпендикуляр ОМ - проекция наклонной. Теорема о 3-х перпендикулярах: Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной. ⇒
АВ⊥КМ и ∠КМВ=90°
б) ВМ перпендикулярна двум пересекающимся прямым КМ и ОМ на плоскости КМО ⇒ ВМ перпендикулярна плоскости КМО, и длина отрезка ВМ - расстояние от т.В до плоскости ОКМ.
∆ ВКМ прямоугольный. ВМ=КМ•tg30°=√3•(1/√3)=1
—————————
2. В ∆ АВС АС=ВС=10 см. ⇒∆ АВС - равнобедренный.
Угол А при основании равнобедренного ∆ АСВ равен углу В=30°. ⇒
угол С=180}-2•30°=120°
а) Расстояние от D до прямой АС - длина перпендикуляра DН, проведенного из D к прямой АС.
DH⊥АС. Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной. ⇒
∆ ВНС -прямоугольный.
Угол ВСН=180°-угол ВСА=180°-120°=60°(смежный углу С)
ВН=ВС•sin60°=10•√3/2=5√3
Т,к. BD перпендикулярна плоскости АВС, она перпендикулярна любой прямой, лежащей в той же плоскости. ∆ DBH- прямоугольный.
По т. Пифагора
DH=(√BD*+BH*)=√(25+75)=10 см.
Плоскости DBH и DHC перпендикулярны. (Если одна из двух плоскостей проходит через прямую (BD), перпендикулярную другой плоскости (ABH), то такие плоскости перпендикулярны.)
Расстояние от точки до плоскости - это длина перпендикуляра, опущенного из заданной точки к заданной плоскости.
Искомое расстояние - расстояние от вершины прямого угла В до гипотенузы ∆ ВDH, т.е. равно высоте, проведенной к гипотенузе.
S (BDH)=0,5•BD•BH
S (BDH)=0,5•BK•DH⇒
BD•BH=BK•DH
5•5√3=BK•10⇒
BK=2,5√3 см.