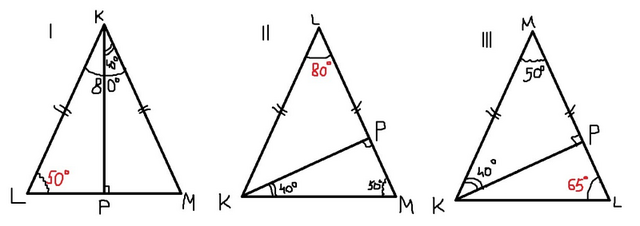
Рассмотрим 3 случая:
I. Высота опущена к основанию.
1. Так как KP - высота, то по свойству она и биссектриса, а значит, ∠K = 40° * 2 = 80°
2. По свойству, ∠L = ∠M. Пусть он равен x, тогда по теореме о сумме углов треугольника 2x+80 = 180 ⇒ 2x = 100 ⇒ x = 50°
II. Высота опущена к боковой стороне, ∠L между ними.
1. Рассмотрим ΔKPM - прямоугольный
∠M = 90 - 40 = 50°, тогда ∠K = ∠M = 50°, так как они при основании равнобедренной трапеции
2. По теореме о сумме углов треугольника ∠L = 180 - 2 * 50 = 80°
III. Высота опущена к боковой стороне, ∠L при основании.
1. Рассмотрим ΔKPM - прямоугольный
∠M = 90 - 40 = 50°
2. По свойству, ∠L = ∠K. Пусть он равен x, тогда по теореме о сумме углов треугольника 2x+50 = 180 ⇒ 2x = 130 ⇒ x = 65°
Ответ: 50°, 65° или 80°