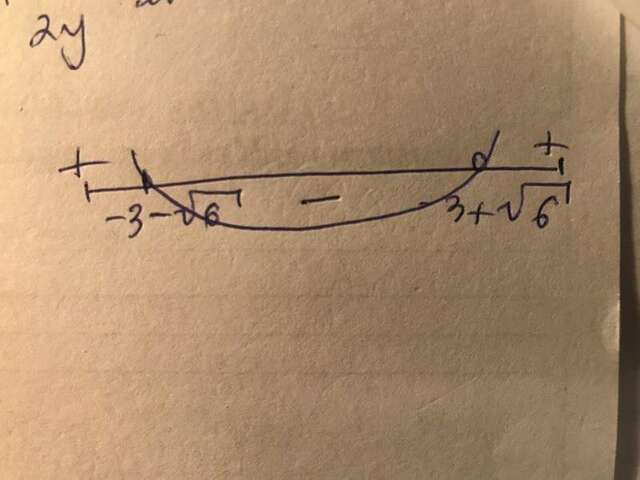≥0.
Т.к. числитель является числом постоянным (а именно отрицательным), то чтобы данное неравенство выполнялось нужно, чтобы знаменатель был отрицательным и не равен нулю. Т.е. (x+3)²-6<0. <br>(x+3)²-6<0<br>x²+6x+9-6<0<br>x²+6x+3<0<br>D=6²-4*3=36-12=24.
x1=

=-3+√6
x2=

=-3-√6
Далее чертим параболу как на рисунке. Ветви параболы направлены вверх(коэффициент при x² положителен), и проходит она через эти две точки(при чём точки выбиты, т.к. неравенство строгое). Мы можем видеть, что - будет на промежутке x∈(-3-√6;-3+√6).
ОТВЕТ: x∈(-3-√6;-3+√6).