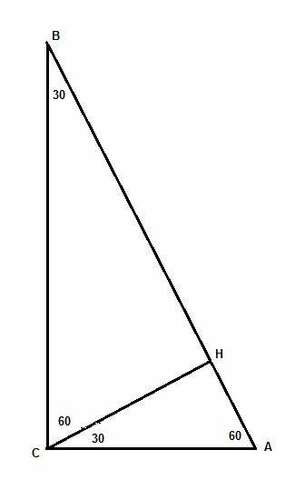
Треугольник изображен на рисунке.
Если высота CH делит прямой угол в отношении 1:2, то это 30° и 60°.
Значит, и сам треугольник имеет углы 30°, 60° и 90°.
Катет AC против угла B = 30° равен половине гипотенузы AB.
AC = AB/2
Второй катет
BC = AB*√3/2
Площадь равна половине произведения катетов
S = AC*BC/2 = 1/2*AB/2*AB*√3/2 = AB^2*√3/8 = 23 - √23
AB = √[8(23 - √23)/√3] = 2√(2/√3)*√(23 - √23) - это длина гипотенузы.
С другой стороны, площадь равна половине произведения основания (гипотенузы) треугольника на его высоту.
S = AB*CH/2
23 - √23 = 2√(2/√3)*√(23 - √23)*CH/2 = √√(4/3)*√(23 - √23)*CH
Высота
CH = √(23 - √23)/(√√(4/3))