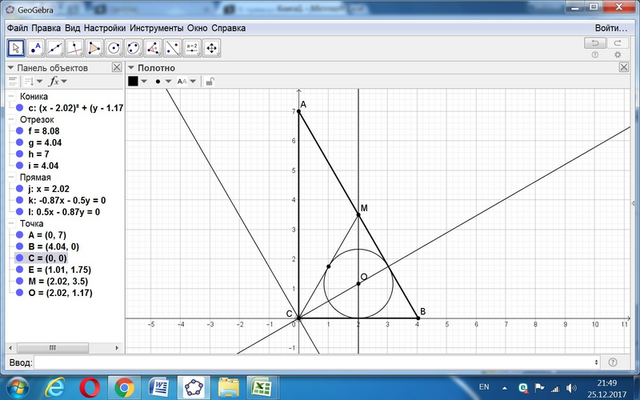
Имеем прямоугольный треугольник АВС (< C = 90°) и медиану СМ.
В треугольник СМВ вписана окружность так, что СМ делится пополам.
По свойству прямоугольного треугольника СМ равна половине гипотенузы АВ, то есть СМ = МВ.
По свойству касательных и условия, что СМ делится пополам,делаем вывод, что в треугольнике СМВ точки касания делят его стороны на равные отрезки.
То есть треугольник СМВ - равносторонний, острый угос В равен 60 градусов.
Ответ: меньший острый угол равен 90 - 60 = 30 градусов.