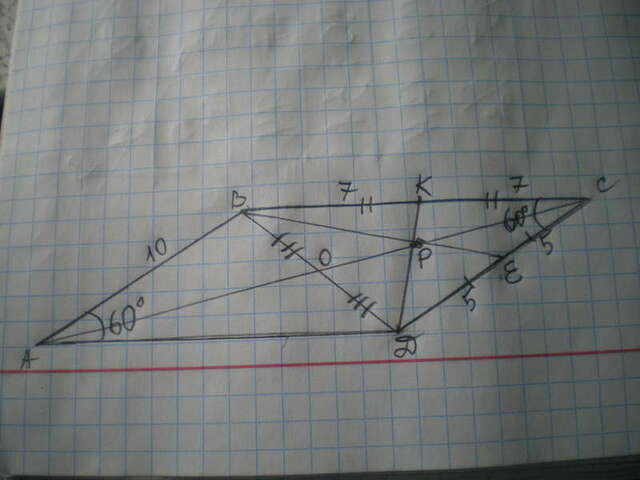
Проведем диагональ ВД и рассмотрим треугольник ВСД.
ВЕ является медианой, т.к. делит пополам сторону СД.
Медианой Δ ВСД является и СО, т.к. по определению в точке пересечения диагонали параллелограмма делятся пополам.
Тогда ДК также является медианой, потому что проходит через точку пересечения двух других медиан.
Отсюда СК=ВК=7 см, а ВС=7*2=14 см.
СД=АВ=10 см.
Найдем площадь ВСД:
S=1\2 * СД * ВС * cos∠C=1\2 * 14 * 10 * (√3\2) = 35√3 см²
Площадь АВСД=2*35√3=70√3 см².
Ответ: 70√3 см².