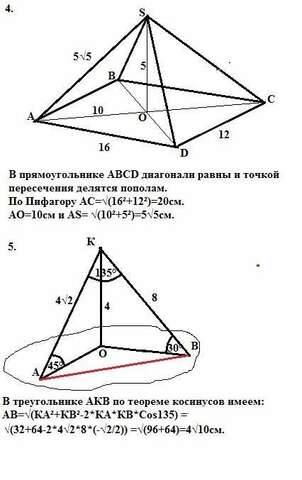
4. В прямоугольнике АВСD диагонали равны и точкой пересечения делятся пополам. Точка F равноудалена от вершин прямоугольника, то есть мы имеем пирамиду, в которой вершина F проецируется в точку пересечения диагоналей прямоугольника.
По Пифагору диагональ АС=√(16²+12²)=20см.
АО=10см и AS= √(10²+5²)=5√5см.
Расстояние от точки F (вершины пирамиды) до вершин прямоугольника (ребра пирамиды) равно 5√5см.
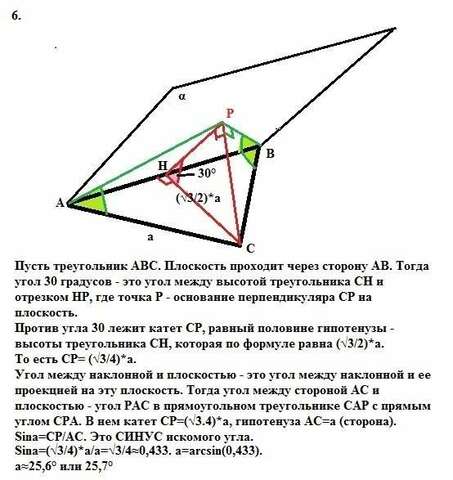
5. Пусть наклонные КА и КВ.Проекция точки F на плоскость - точка О. Тогда в прямоугольном треугольнике АОК с острым углом 45° катеты равны 4см и гипотенуза (наклонная) КА=4√2см.
В прямоугольном треугольнике ВОК против угла 30° лежит катет КО=4см. Значит гипотенуза (наклонная) КВ=8см.
В треугольнике АКВ по теореме косинусов имеем:
АВ=√(КА²+КВ²-2*КА*КВ*Cos135) =√(32+64-2*4√2*8*(-√2/2)) =√(96+64)=4√10см.
Ответ: расстояние между точками А и В равно 4√10см.
6. Пусть треугольник АВС. Плоскость α проходит через сторону АВ. Угол между двумя пересекающимися плоскостями равен углу между прямыми, по которым они пересекаются с любой плоскостью, перпендикулярной их линии пересечения.
Опустим на плоскость α перпендикуляр СР и проведем через этот перпендикуляр плоскость, перпендикулярную стороне АВ (линии пересечения плоскостей АВС и α - ребру двугранного угла между плоскостями.
Тогда угол 30 градусов - это угол между высотой треугольника СН и отрезком НР, где точка Р - основание перпендикуляра СР на плоскость.
Против угла 30 лежит катет СР, равный половине гипотенузы - высоты треугольника СН, которая по формуле равна (√3/2)*а.
То есть СР= (√3/4)*а.
Угол между наклонной и плоскостью - это угол между наклонной и ее проекцией на эту плоскость. Тогда угол между стороной АС и плоскостью - угол РАС в прямоугольном треугольнике САР с прямым углом СРА. В нем катет СР=(√3/4)*а, гипотенуза АС=а (сторона). Sina=CР/АС. Это синус искомого угла.
Sina=(√3/4)*а/a=√3/4≈0,433.
а=arcsin(0,433). a≈25,6° или 25,7°.