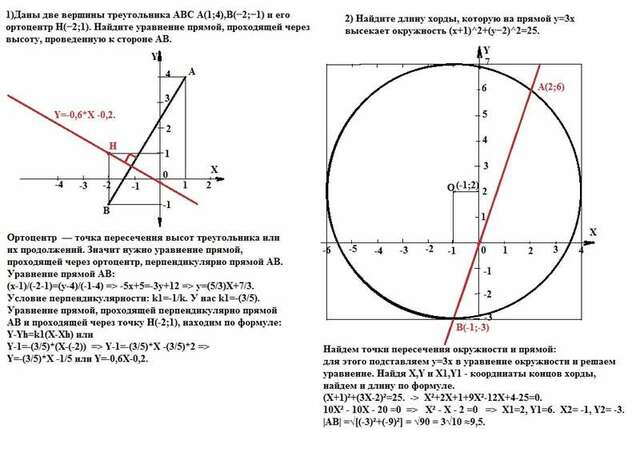
1) Определение: "Ортоцентр - точка пересечения высот треугольника или их продолжений". Значит нам нужно уравнение прямой, проходящей через ортоцентр, перпендикулярно прямой АВ.
Уравнение прямой АВ:
(x-1)/(-2-1)=(y-4)/(-1-4) => -5x+5=-3y+12 => y=(5/3)X+7/3. k=(5/3).
Условие перпендикулярности прямых: k1=-1/k. У нас k1=-(3/5).
Уравнение прямой, проходящей перпендикулярно прямой АВ и
проходящей через точку Н(-2;1), находим по формуле:
Y-Yh=k1(X-Xh) или
Y-1=-(3/5)*(X-(-2)) => Y-1=-(3/5)*X -(3/5)*2 =>
Y=-(3/5)*X -1/5 или Y=-0,6X-0,2.
2) Найдите длину хорды, которую на прямой y=3x высекает
окружность (x+1)^2+(y−2)^2=25.
Найдем точки пересечения окружности и прямой:
для этого подставляем значение y=3x в уравнение окружности и решаем уравнение. Найдя Х1,Y1 и X2,Y2 - координаты концов хорды, найдем и ее длину (модуль) по формуле:
|AB| =√[(Xb-Xa)²+(Yb-Ya)²]. Итак:
(X+1)²+(3X-2)²=25. -> X²+2X+1+9X²-12X+4-25=0.
10X² - 10X - 20 =0 => X² - X - 2 =0 =>
X1= 2, Y1= 6.
X2= -1, Y2= -3.
|AB| =√[(-3)²+(-9)²] = √90 = 3√10 ≈9,5.
Решение проверим, построив графики.