Помогите пожалуйста решить. В трапеции MNPK ( MK NP ) продолжения боковых сторон MN и KP...

Question

Помогите пожалуйста решить.
В трапеции MNPK ( MK NP ) продолжения боковых сторон MN и
KP пересекаются в точке Т. а) Докажите, что треугольники NTP и
MTK подобны. б) Найдите площадь треугольника TMK, если известно, что TN : NM = 5 : 3, а площадь треугольника NTP равна 75.

Answer 1

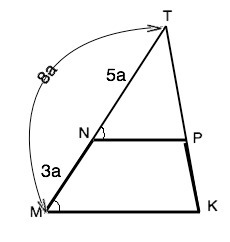
Основания трапеции параллельны. 

В ∆ NTP и ∆ МТК угол Т общий, соответственные углы при пересечении параллельных МК и NP секущей ТМ равны. 

 ∆ NTP подобны ∆ МТК по первому признаку подобия. 

k=TM:TN= (5+3):5

Отношение площадей подобных треугольников равно квадрату коэффициента их подобия. 

S (MTK):S (TNP)=8²: 5²=64:25

S (MTK):75=64:25⇒

S (MTK)=64•3=192 (ед. площади)

---