ABCDA1B1C1D1 - куб. Точка N - середина ребра BB1, а точка M - середина отрезка BD....

Question

ABCDA1B1C1D1 - куб. Точка N - середина ребра BB1, а точка M - середина отрезка BD. Найдите tg^2a, где a -угол между прямой, содержащей MN, и плоскостью(A1B1C1D1).

Comments

да, хорошо.

Answer 1

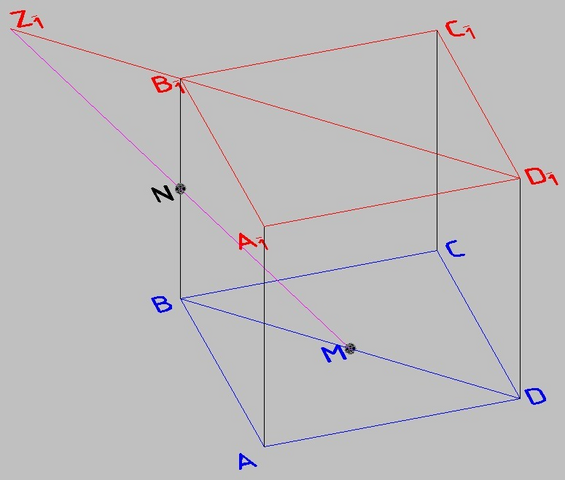
Угол, под которым пересекается прямая MN с верхней плоскостью куба, равен углу, под которым эта прямая пересекается с нижней плоскостью куба в силу параллельности этих плоскостей.
a - ребро куба
BM = 1/2*BD = a√2/2 = a/√2
BN = 1/2*a
tg(∠BMN) = BN/BM = 1/2*a / (a/√2) = √2/2 = 1/√2
В ответе требуют квадрат тангенса
tg²(∠BMN) = (1/√2)² = 1/2

---