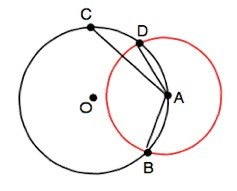
Допустим, что такие четыре точки существуют и из одной точки окружности проведены три разные хордыравной длины.
Если из точки А как из центра провести вторую окружность радиусом, равным длине этих хорд, то по определению окружности точки В, С и D, равноудаленные от центра А, будут лежать и на второй окружности. Тогда две окружности пересекутся в трех точках. Это противоречит теореме:
Окружность и прямая, а также две окружности могут пересечься не более, чем в двух точках.