Трапеция ABCD (AB||CD) лежит в плоскости альфа, АВ = 9 см. Вне плоскости альфа взяли...

Question

Трапеция ABCD (AB||CD) лежит в плоскости альфа, АВ = 9 см. Вне плоскости альфа взяли точку М и на отрезке АМ отметили такую точку К, что АК:КМ=2:1. Точка F - точка пересечения плоскости (DKC)и отрезка МВ. Найдите длину отрезка KF. a)30см б)45 в)4,5 г)3 д)3,5 с чертежом плиз

Answer 1

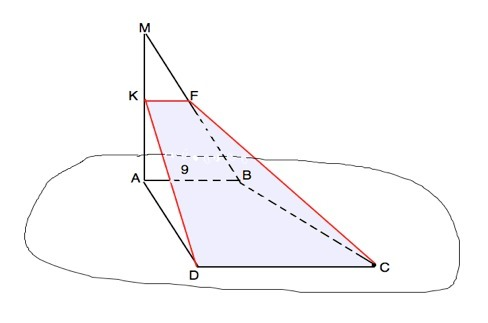
Теорема:Если через каждую из двух параллельных прямых проведена плоскость, причем эти плоскости пересекаются, то линия их пересечения параллельна каждой из данных прямых.

Плоскость АМВ проходит через АВ, плоскость DKC проходит через DC. 

АВ||СD⇒ KF||AB||CD 

В ∆ KMF сторона KF параллельна АВ⇒ соответственные углы при при основаниях треугольников KMFи АМВ равны, угол М - общий. ⇒

Δ KMF~ ΔАМВ с коэффициентом подобия АМ:КМ=(2+1):1 ⇒ k=3:1 

АВ:KF=3:1 ⇒

KF=9:3=3 см

---