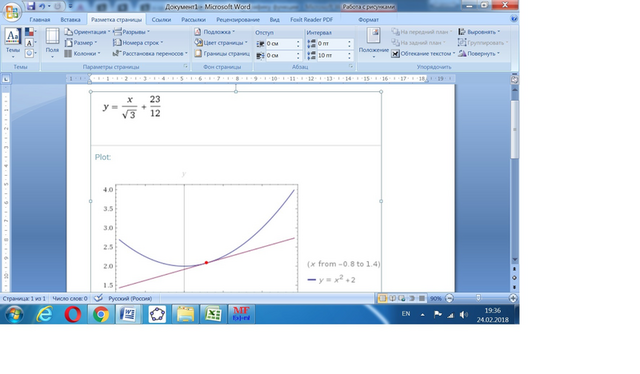
Угловой коэффициент касательной равен производной функции в данной точке.
Производная функции y = x² + 2 равна y' = 2x.
Приравняем 2х = tg 30° = 1/√3.
Отсюда находим абсциссу точки касания: х = 1/(2√3) = √3/6 ≈ 0,288675.
Функция в этой точке равна:
у = (3/36) + 2 = (1/12) + 2 = 25/12 ≈ 2,083333.
Уравнение у(кас) = (1/√3)*(х - (√3/6)) + 2 = (√3/6)*х + (23/12).