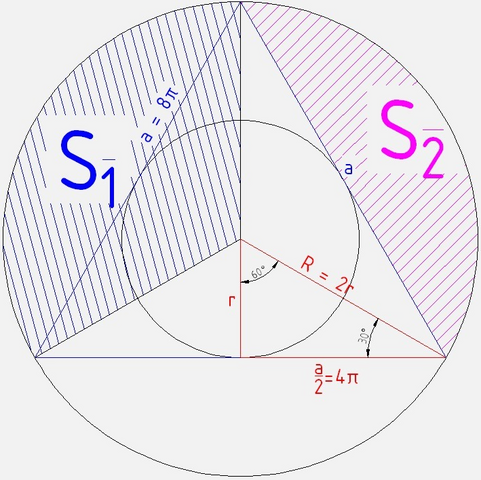
Сторона треугольника равна 24π/3 = 8π см
Рассмотрим красный прямоугольный треугольник на рисунке
Половина этой стороны - катет, длина его 4π см
второй катет - радиус вписанной окружности r, лежит против угла в 30 градусов и его длина в 2 раза короче гипотенузы
Гипотенуза является радиусом описанной окружности R
По Пифагору
(4π)² + r² = (2r)²
16π² = 3r²
r² = 16/3*π²
r = 4π/√3 см
R = 2r = 8π/√3 см
угол при вершине сегмента β=120°
Площадь сектора S₁ (синяя штриховка на рисунке)
S₁ = πR²*β/360° = π*(8π/√3)²*120°/360° = π*64π²/3*(1/3) = 64/9*π³ ≈ 220,4893 см²
Площадь сегмента S₂ (малиновая штриховка на рисунке)
S₁ = πR²*β/360°-1/2*R²*sin(β) = π(8π/√3)² *120°/360°-(8π/√3)²/2*√3/2 = 64π²/3*(π/3 - √3/4) ≈ 129,3177 см²