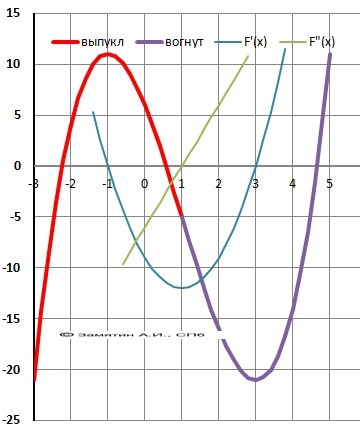
Рисунок к задаче в приложении.
Посмотрите, какая красота - одна производная переходит в другую.
ДАНО
F(x) = 1/3*x³ - 3*x + 5 - уравнение пути.
Пусть Х- это ВРЕМЯ.
РЕШЕНИЕ
Скорость - первая производная пути
V(x) =S'(x) = x² - x - 3 - уравнение скорости
Ускорение - первая производная скорости и вторая от пути.
a(x) =V'(x)=S"(x) = 2*x - 1 - уравнение ускорения.
Но оказывается, что оно зависит от времени.
Найдем ещё одну производную - скорость измерения ускорения.
z(x) = a'(x)=S"'(x) = 2 - постоянная.
А теперь вернёмся к слову ПРИМЕНЕНИЕ производной в нашей жизни.
В нашем примере у функции есть - скорость ускорения.
Какое-такое физическое явление можно представить - КОСМОС.
Как много в этом слове заключено НЕПОЗНАННОГО.